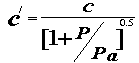|
TL stuffing density
calculations
In popular literature
of the TL (1) the following equation is given, that relates stuffing density
to the change of speed of sound:
|
|
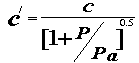
where
c = 344 m/sec speed of sound in air
P = packing density of fibrous material
Pa = 1.18kg/m3, density of air. |
Now if we set P
= Pa, the case of an unstuffed line, note c' = c only
if we set c =  ,
so that there appears to be an error in the equation as given, however once c'
is computed what does it mean or how are we to utilize it to define Dt,
the stuffing density for a specific line length.
Using the example of TLB
where optimum Dt = 0.6 for wool, c' calculates to 129.8 m/sec,
or an alpha ratio of 0.377
However what is not apparent in the equation and is clearly shown that P/Pa
ratio or Dtr is an function of w, thus fiber type dependent,
and more importantly that there is an implicit limit to the possible change of sound
velocity in the fiber mass and thus the D phase for the Terminus signal.
By correlating the measured data, phase of Fr @ woofer response near field
to that of the Terminus at optimum fiber density to the calculated 1/a
we get an estimate of the phase shift required for a range of TL line lengths. To
do this we use empirical TL stuffing density data as given in the following plot. |
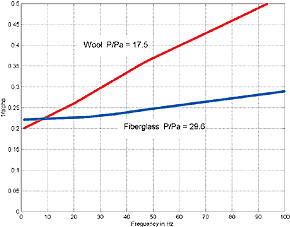
Fig 1 Wool vs Fiberglass
Fiber data
click image for larger chart
|
|
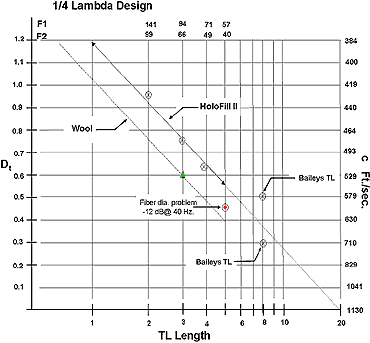
Fig 2
click image for larger chart
|
|
The data shows that from
line lengths 2 ft (0.61 m) to 4 ft (1.22 m) the Dtr varies linearly from
12.2 to 8.1 for Dacron HoloFill II fiber. For wool the figures would be 30% less.
The correlated data is presented in Table 03. |
Table 03.
Fiber Density Terminus Phase Shift*
|
|
Line
length
(m)
|
Fr
(Hz)
|
Dtr
|
Wf
|
Tf
|
D Tf
|
|
|
0.610
|
141.0
|
12.2
|
|
|
|
|
0.914
|
94.0
|
|
|
|
|
|
1.220
|
70.6
|
|
|
|
|
|
1.520
|
56.6
|
|
|
|
|
*
missing data is being recreated from the original data |
(1) LSDC, chapter 4,.pg.75 Table 4.2
|
