Phase Data

The TL's system response (1 meter measurement) is the vector summation of the near field woofers response and the near field Terminus response. Since vector summation requires magnitude and phase, the following data sample is used to illustrate this relationship.

The woofer magnitude and phase can be modeled as a small signal response for Qtc=0.5 close box response. Mathematically this can be described by the Beranek equations of a Plane Circular Piston in Infinite Baffle (1). This implies a linear phase response. While in a general case there are serious problems with this model, this is close to what is measured for the TL36, Fig. 1. Note that for Fr=60 Hz the phase angle = -80° and magnitude = -8 dB. It should be noted where the phase transition occurs, vs that of the terminus response in Fig.2. 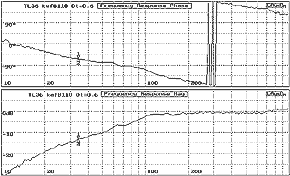Fig. 1 TL Terminus response for a line Dt=0.6, Dacron HoloFill II fiber click image for larger charts Corresponding to the near field woofer response is the near field Terminus response, Fig. 2. The Terminus response for Fr = 60 Hz the phase angle = +19.3° and magnitude = -3.8 dB. The measured magnitude has a 20 dB attenuation, thus the reference magnitude is 20-3.8 = +16.2 dB in reference to the near field woofer measurement. The D phase ~99° is very close to the TL system requirement of 90° for maximum gain @ Fr. From this we can infer that the Dt is close to optimum for the fiber type used. To relate the phase of Fig.2 vs Fig.1, you have to compare the front of the woofer's response to that of the back of the woofer's response, ie the interior of the TL line, shown in Fig.5. For the Terminus the phase transition does not occur at the line resonance frequency Fr related to the 1/4l, but at the 2nd harmonic frequency. This is important in analyzing the nulls in the TL system response and the shift with frequency with stuffing density change. 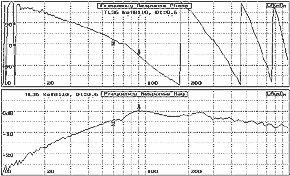Fig. 2 TL Terminus Response, Magnitude and Phase click image for larger charts

______________________________________________________________________________________ (1) Acoustics, L. Beranek, Section 5. pg 118.

Unstuffed Line Response

To gain an understanding of the TL Terminus change with Dt it is useful to examine the Terminus response for the unstuffed line since it is the limiting case and one gains an understanding of the 1/4l TL line resonance definition.

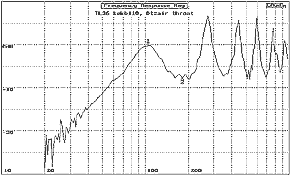
Fig.3 TL 36 TL Line Harmonics, Terminus Response, Dtr = 1.0 click image for larger chart The TL line length is characterized by Fr, the line 1/4 l resonance frequency and the associated harmonics. Two interesting effects of the Terminus response for the unstuffed line are apparent in the plot of Fig. 3: The low frequency attenuation slope, -18 dB/octave. The asymptotic attenuation of the harmonics. From the asymptotic attenuation of the harmonics we can infer that even for the unstuffed line, Dtr=1, air at a density of 1.18kg./m3, the attenuation function is non-linear with frequency.

Thus we can infer that with fiber having a greater density than air, a more pronounced attenuation function as well as a change in air velocity in the fiber mass will occur

Table 01 TL 0.91 meters, Dtr = 1   Calculated Measured Shift Magnitude     Type (Hz) (Hz) (Hz) (dB) Phase Transitions *Fr 94.2 104.3 +12.1  +8.6% +0dB -56.5°   1st Harmonic 188.3 180.8 -7.5  -4.0% -7.6dB -159°   2nd Harmonic 282.5 273.2 -9.3  -3.3% +6.8dB +80.9° 233.5 3rd Harmonic 376.7 352.8 -23.9  -6.3% -7.3dB -10.3°   4th Harmonic 470.9 446.6 -24.3  -5.2% +5.7dB -134° 464.6 5th Harmonic 565.0 533.1 -31.9  -5.7% -8.1dB +151°   6th Harmonic 659.2 599.8 -59.4  -9.0% +6.7dB +66.5°   7th Harmonic 753.4 688.3 -65.1  -8.6% -7.6dB -34.5°   8th Harmonic 847.6 774.5 -73.1  -8.6% +3.7dB -116° 789.9 9th Harmonic 941.7 871.4 -70.3  -7.5% -6.4dB +145° 10th Harmonic 1035.9 924.4 -111.5  -10.8% +1.0dB +56.7°   Note the shift in frequency of the measured peak values from the calculated. This is not an instrumentation problem but the byproduct of speed of sound shift.

* For TLB the Fr for the unstuffed line @ 104 Hz moves to ~ 65 Hz= as shown in Fig.5.2, TLB system response when stuffed. This is one of the differences from the generic TL line where the Fr shift due to fiber density would be much smaller.

Stuffed Line Response

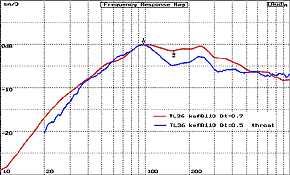
Fig. 4 TL 36 Terminus Response Dtr = 6.8/ Dtr = 9.5 click image for larger chart Fig. 4 shows the progressive change in the bandwidth of the Terminus with the change of Dtr. Note that the low frequency slope hinge point at 1/4l does not change, this is a function of line length. However the bandwidth from the 1/4l frequency changes: the high end -3 dB point moves to a higher frequency and the odd harmonic nulls are attenuated. These factors are a function of the fiber attenuation characteristics defined by Bradbury's equations. It is interesting to compare the low frequency response of the interior of the TL line, ie the back of the woofer, Fig. 5 to that of Fig. 4. In summary the high frequency slope point is set by line length, however the low frequency slope frequency changes with stuffing density. As the density is increased it approaches the fundamental of a pressure response.

The TL's Interior response, ie back of the woofer's spectral response, as shown in Fig.5 documents that contrary to the popular conception that it is a mirror image of the front of the woofer, it is fundamentally changed by the TL's line loading and is essentially a pressure phenomena. This phenomena is complex and not discussed further in this document. Note that the phase from DC to the 1/4l frequency is linear. This sets the phase response of the Terminus, though for the Terminus the additional factor of frequency change vs. fiber density and type has to be added. 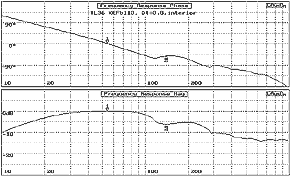Fig. 5. TL Line, Interior Response click image for larger chart

[ Back to the Transmission Line Speaker Page | The TLB | Appendix TOC ]